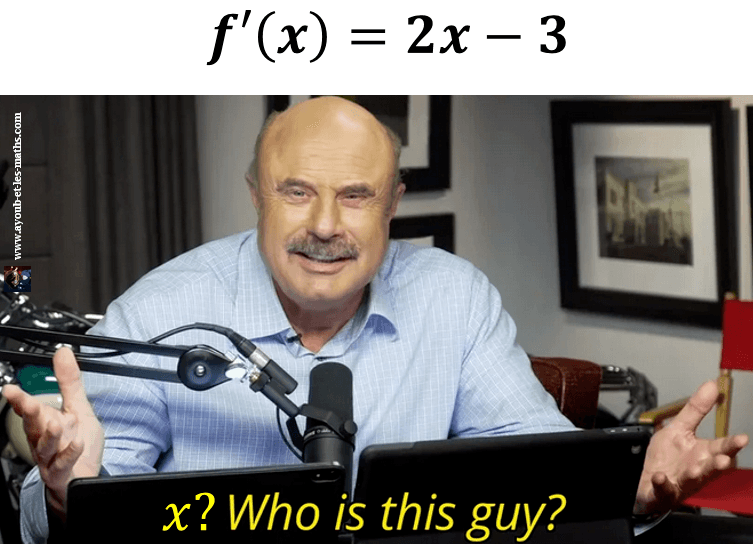Lorsque, dans une discussion, on désire faire intervenir un nouvel acteur, les présentations doivent être faites correctement. En mathématiques comme dans la vie de tous les jours, la courtoisie compte. Si l’énoncé nous demande par exemple de déterminer la dérivée f’ d’une certaine fonction f donnée par l’énoncé, commencer la rédaction brutalement par « f'(x) = …. » traduit au mieux une blâmable désinvolture.
Au-delà du fait qu’une justification (même brève) de la dérivabilité est toujours la bienvenue, le lecteur de notre rédaction pourrait poser, à juste titre, la question suivante : mais quel est donc ce x dont vous me parlez, et en lequel vous évaluez f’ ? Il est aussi désagréable de voir surgir ce x sans aucune explication que de voir apparaître, au détour d’un roman qu’on lisait jusque là avec attention : « Henri s’exclama… », sans que l’auteur n’ait fait l’effort de présenter ledit Henri auparavant.
D’où l’utilité de placer un petit « ∀ x ∈ ℝ, … » (si la dérivée est définie sur ℝ) juste avant le calcul. Notre lecteur comprend alors que pour tout x appartenant à ℝ, f'(x) = …, et la question de quel x me parlez-vous donc ? devient obsolète. De même, si on veut exprimer l’idée que 3 a un antécédent par la fonction f, se contenter d’écrire f(x) = 3 nous attirerait les foudres de ce lecteur attentif. Encore une fois, qui est ce x ? Par contre, en précisant soigneusement « ∃ x ∈ ℝ, f(x) = 3″, nous évitons cette prise de bec avec le correcteur, qui comprend « il existe un réel x tel que f(x) = 3, c’est-à-dire dont 3 est l’image par f ». x est alors présenté correctement et peut intervenir dans la discussion.
La tolérance face à l’oubli des quantificateurs dépend du niveau et du lieu. Beaucoup d’enseignants au lycée laissent passer de tels oublis lorsque les intentions de l’élève sont compréhensibles, pour ne pas trop le pénaliser. Mais c’est avec une salve de traits rouges rageurs que l’étudiant nonchalant voit ses oublis accueillis en prépa ou en licence scientifique. Autant se préparer à la rigueur le plus tôt possible…