De l’attachement déraisonnable aux lettres
Un certain nombre d’élèves (ou d’anciens élèves) affirme avoir aimé les mathématiques qui leur étaient inculquées à l’école et au collège, jusqu’à ce que les lettres se mettent à côtoyer les nombres (calcul littéral notamment). Le franchissement de ce palier d’abstraction peut laisser un souvenir cuisant. Malheureusement, il ne constitue qu’une première étape dans ce rapport plus ou moins conflictuel qu’établissent les élèves avec l’utilisation des lettres en mathématiques.
La détestation de ces dernières laisse paradoxalement place à une confiance aveugle qui leur est accordée, favorisée par le funeste oubli qu’une lettre ne vaut que par ce qu’elle représente. Ce que nous appelons confiance aveugle, c’est notamment cette propension de l’élève à associer telle lettre de manière abusive à tel concept qu’elle représente généralement. F ? Forcément une primitive de f. Delta ? Nécessairement un discriminant. u ? C’est une suite ! Une matrice P ? Elle est forcément inversible, du coup!
Un tel attachement à la lettre se ressent dans l’apprentissage du cours, et plus précisément dans l’assimilation de certaines formules. Tenez, par exemple, la somme de termes consécutifs d’une suite géométrique… Même lorsque l’élève vous fait le plaisir de se souvenir que, pour appliquer ladite formule, la raison q doit être différente de 1, et qu’il n’oublie pas le premier terme en facteur, il ânonnera très souvent :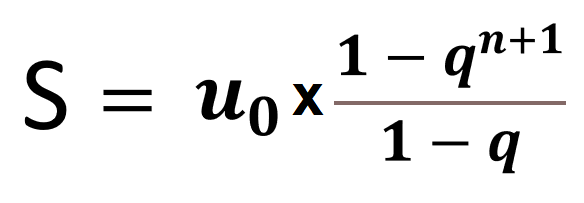 Oui mais qui est n ? Pourquoi n+1 ? Effectivement, pour des puissances allant de 0 à n, cela est valable. Mais si l’on change le nombre de termes, la formule ainsi apprise devient obsolète. Lorsque l’on apprend une formule avec des lettres, il faut s’assurer de bien comprendre ce que chacune représente. Il vaut mieux retenir, au lieu de l’exposant n+1, qu’il faut mettre le q du numérateur à la puissance « le nombre de termes dans la somme ».
Oui mais qui est n ? Pourquoi n+1 ? Effectivement, pour des puissances allant de 0 à n, cela est valable. Mais si l’on change le nombre de termes, la formule ainsi apprise devient obsolète. Lorsque l’on apprend une formule avec des lettres, il faut s’assurer de bien comprendre ce que chacune représente. Il vaut mieux retenir, au lieu de l’exposant n+1, qu’il faut mettre le q du numérateur à la puissance « le nombre de termes dans la somme ».
Non contente d’entraver son apprentissage du cours (en limitant son efficacité aux situations où ce seraient exactement les mêmes lettres et les mêmes situations qui tomberaient en examen), cette confiance aveugle en la lettre a des effets particulièrement néfastes sur sa rédaction. Ainsi, lorsqu’on lui demande une primitive de f sur un intervalle donné, il ne s’embarrasse pas de balancer F(x) = …, sans préciser nulle part que F est une telle primitive. « Mais c’est évident, non ? Bah, le correcteur comprendra. » Ou encore, il écrit q sans l’avoir présenté, laissant toujours au correcteur le soin d’interpréter q comme la raison d’une certaine suite géométrique. Associée à une absence de quantificateurs, cette désinvolture peut rendre certaines copies très désagréables à corriger (et vous n’avez surtout pas envie que votre correcteur trouve votre copie désagréable).
Bien évidemment, dans certains cas, l’entendement fait que nous ne nous étalons pas sur la signification de telle lettre utilisée (introduction de Delta juste après avoir présenté un trinôme du second degré, par exemple). Mais, dans le doute, veillez toujours à ce que les lettres que vous employez ne constituent pas un écran de fumée; qu’elles aient un sens, et qu’il soit bien compris du destinataire de votre travail, sans que ce dernier doive fournir l’effort de le deviner.
