Retour sur un piège réussi
Il se frotta frénétiquement les yeux, puis les mains. La réussite de son piège dépassait toutes ses espérances. Il avait dissimulé ce trou sous un feuillage dense, tout près d’une hellébore ravissante, que le promeneur de fin d’année ne manquerait pas de vouloir cueillir. Dans un accès d’espièglerie affectueuse, il avait rembourré le fond du trou de plumes douillettes, pour assurer quelque délicatesse à l’impact. Les passants peu avertis chutaient les uns après les autres, tels les feuilles mortes qui jonchaient le sol, en grattant les cordelettes de la terre dans une symphonie bien douce à ses oreilles. Petit bémol, cependant : de nombreuses victimes étaient tombées non pas dans le trou prévu à cet effet, mais, le brouillard aidant, en se prenant les pieds dans les racines d’un arbre majestueux à proximité. Cet arbre qu’il avait juste planté pour faire diversion, afin que l’œil du promeneur imprudent ne décelât pas l’irrégularité chromatique du piège au sol.
Peut-on se réjouir de remporter une partie d’échecs sur un mat imprévu? L’émerveillement que provoque la situation est à même de consoler la froissure d’un égo démesuré qui, non content de triompher, aurait aussi aimé prévoir les conditions exactes du triomphe. Encore faut-il n’avoir pas perdu, dans le blasement généralisé du monde moderne, sa capacité à s’émerveiller…
Trêve de balourdises narratives, et venons-en au fait. Voici un quizz que j’ai récemment proposé à mes « suiveurs » sur un certain réseau social :
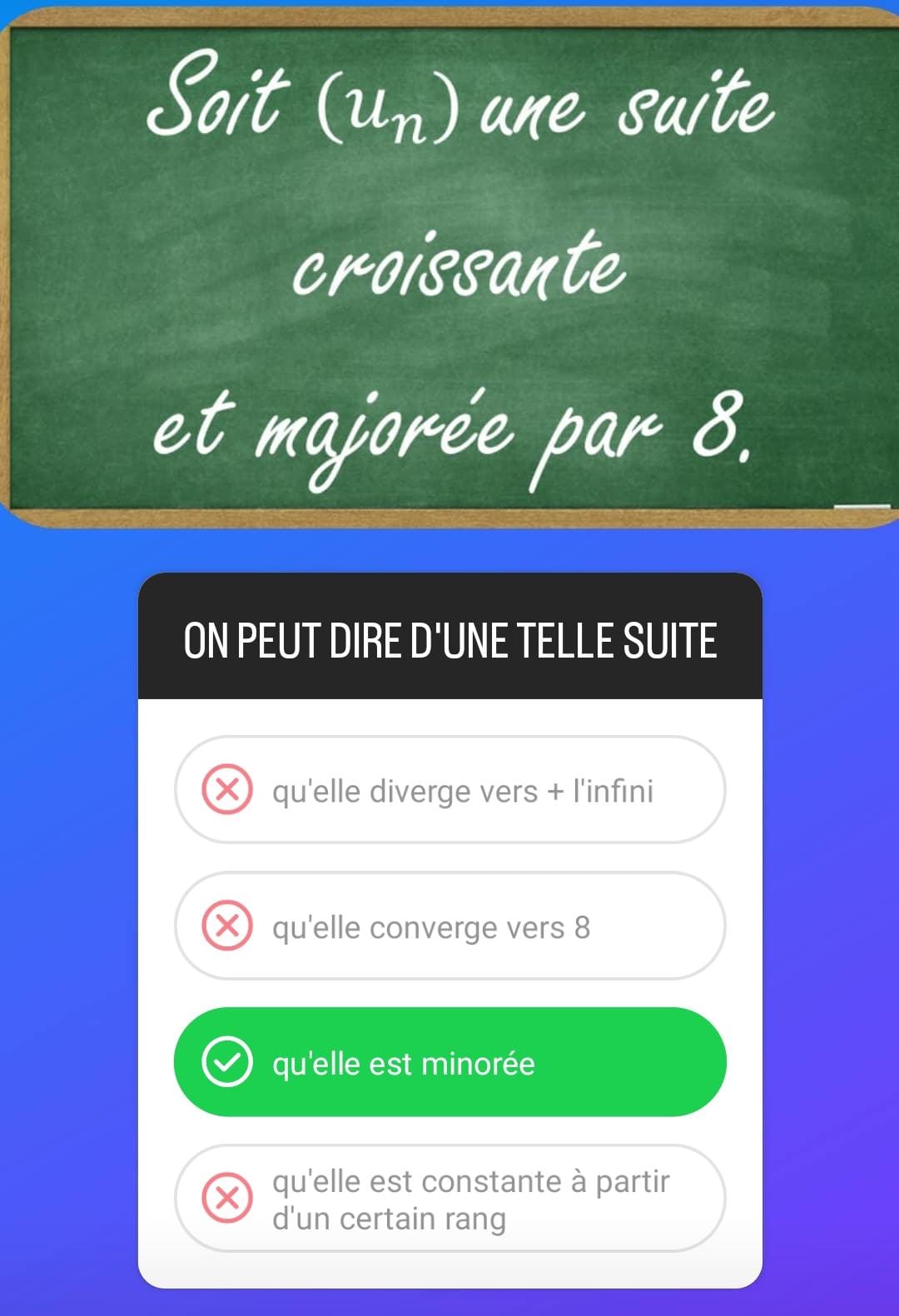
Oui, désolé, je donne la réponse sans crier gare, afin de passer directement à l’idée du piège, et à l’analyse de ce qui a bien pu se produire dans les rangs des votants, pour que les résultats du quizz soient les suivants :
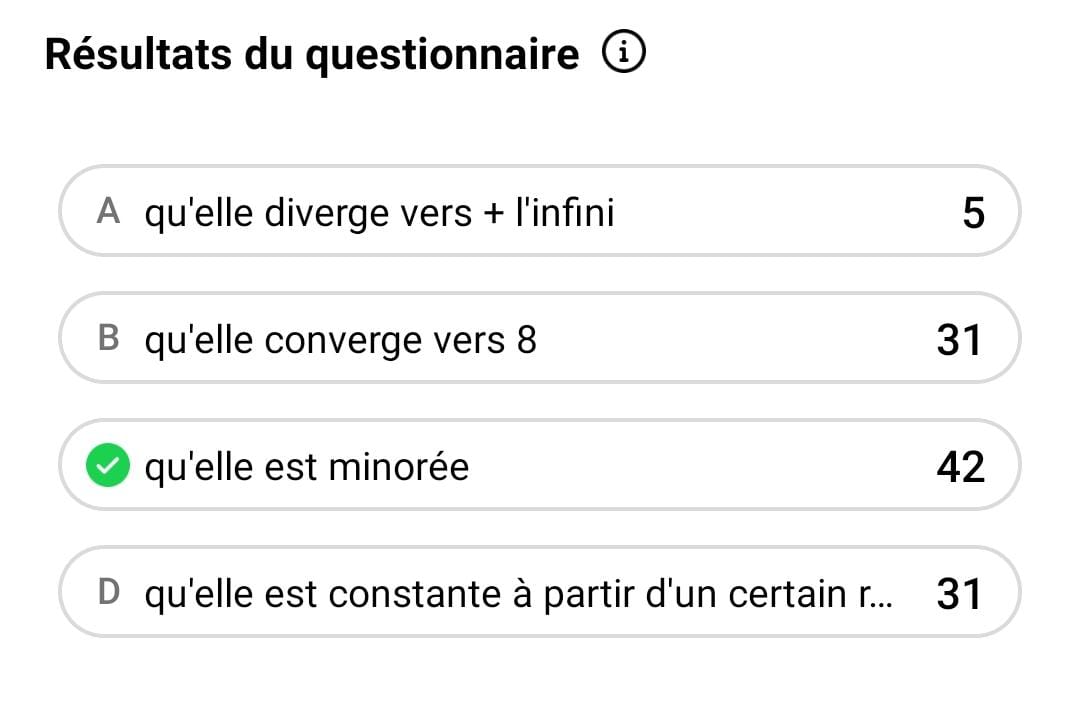
Matérialisé par la réponse B, le piège classique dans lequel je comptais faire tomber une bonne partie des participants s’est avéré, comme à son habitude, plutôt efficace. « Toute suite croissante majorée converge », dit le cours, et ce dès la Terminale. « Toute suite croissante majorée par 8 converge vers 8 », en conclut le lecteur hâtif, qui cède aux violons de la rime facile, pour se retrouver dans le décor. Cher lecteur, une suite croissante majorée par 8 est aussi majorée par 40, 27, 518, et en fait, tous les réels supérieurs ou égaux à 8. Voudrais-tu me signifier que notre suite convergerait vers tous ces nombres à la fois ? Si le théorème de convergence monotone t’assure effectivement de la convergence de cette suite (vers un réel inférieur ou égal à 8), rien ne te garantit, en revanche, dans le cas général, que sa limite est 8. Mon parterre rembourré de plumes donne sommeil, mais ne t’endors pas trop vite; tiens, une échelle.
J’attendais bien moins de monde à la réponse D – et quelle ne fut ma surprise de constater cet attroupement de trébuchants au pied de l’arbre ! Je soupçonne une grande partie d’entre eux d’avoir vu le piège de la B, contre lequel, peut-être, ils ont été avertis un grand nombre de fois. Mais dans leurs esprits trottait, à partir des hypothèses données par l’énoncé, la conclusion suivante « une telle suite converge ». Conclusion parfaitement exacte, mais ne figurant pas parmi les réponses proposées. Il se sont donc rabattus sur la réponse la plus proche, à leurs yeux, de la notion de limite: celle faisant carrément de notre suite une suite stationnaire (constante à partir d’un certain rang). Mais pourquoi donc ? La suite dont parle l’énoncé peut parfaitement être strictement croissante, invalidant ainsi la réponse D.
Réponse C, ma belle hellébore, tu auras finalement été cueillie par un peu plus d’un tiers des votants, qui pourront fièrement t’arborer à la boutonnière. Négligée parce que tu ne fais pas intervenir cette notion de limite, tu ne te sers en fait que d’une partie des hypothèses de l’énoncé : la simple croissance de la suite suffisait à conclure qu’elle est minorée. Entre autres valeurs, par son premier terme… Et bien oui, une suite croissante vous donne la certitude qu’elle ne prendra jamais de valeur strictement en-dessous de son premier terme.
Il me semble permis d’affirmer, sans trop de risque de me tromper, que le fait de ne pouvoir utiliser qu’une partie des hypothèses de l’énoncé chagrine l’inconscient d’un grand nombre d’élèves. L’hypothèse inutilisée cause bien des démangeaisons de l’esprit. Elle est ce boulon mystérieux restant après avoir monté l’armoire, ou réparé le moteur (à titre personnel, je préfère quand c’est l’armoire, les pannes d’armoire étant en général plus faciles à gérer). Mais, dans le cadre d’un contrôle, par exemple, il ne faut pas présager de son utilisation à tel ou tel moment, quitte à inventer une hypothèse supplémentaire qui n’y était pas ! Nombreux sont ceux qui doivent réentendre cette évidence: n’utiliser qu’une partie des hypothèses est tout à fait permis ; ce qui ne l’est pas, c’est d’inventer des hypothèses imaginaires pour pouvoir les combiner à celles que nous avions de manière légale. Ces inventions coupables sont un cas particulier de « concordisme mathématique », notion que j’aborde plus en détail dans cet article.
Ici, bien entendu, l’on pouvait se demander l’intérêt pour moi de rajouter une hypothèse superflue alors qu’il n’y avait pas d’autre question susceptible de l’utiliser derrière. Mais, le simple plaisir de vous piéger, mon enfant.
Fait divers : cinq promeneurs portés disparus. Selon des témoignages divergents, un aigle géant aurait été aperçu tournoyant dans les cieux embrumés, au-dessus de la forêt de Métaflore.
